Геометрические задачи: методы решения и примеры

В современном мире, где все больше и больше процессов зависят от точных научных расчетов, геометрия стоит в центре многих из них. Эта древняя наука, которая изучает формы, размеры и свойства пространственных объектов, играет ключевую роль в нашей повседневной жизни. Каждый раз, когда вы измеряете размер комнаты перед покупкой новой мебели или рассчитываете расстояние для своего следующего путешествия, вы, возможно неосознанно, используете принципы геометрии.

Однако геометрия не ограничивается только простыми измерениями. Она служит основой для решения сложных задач, которые встречаются в различных областях: от архитектуры и дизайна до астрономии и робототехники. Геометрические задачи часто становятся настоящим вызовом даже для профессионалов в области науки и техники.

В этой статье мы рассмотрим различные методы решения геометрических задач, а также приведем конкретные примеры их применения. Надеемся, что данный материал поможет вам лучше понять и освоить эту увлекательную область математики.

Основные методы решения геометрических задач

Геометрия – это не только про фигуры и линии; это наука, в которой глубоко проработанные методы позволяют решать разнообразные задачи. В зависимости от специфики задания и желаемого результата существует несколько основных методов решения геометрических проблем.

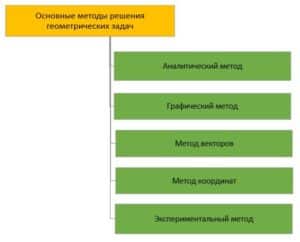
• Аналитический метод: Этот метод основан на использовании алгебраических выражений для описания геометрических свойств и отношений. Представьте, что геометрия встречается с алгеброй, и в результате этой встречи рождается решение. Аналитический метод идеален для задач, где требуется точное и логическое рассуждение.
• Графический метод: Для визуальных мыслителей и тех, кто предпочитает «видеть» решение. Здесь геометрические фигуры и объекты рисуются и анализируются вручную или с помощью программного обеспечения. Этот метод позволяет быстро оценить и интерпретировать геометрические связи.
• Метод координат: Введение системы координат позволяет преобразовать геометрические задачи в алгебраические. Хотите определить расположение точки или выразить прямую через уравнение? Этот метод для вас.
• Метод векторов: Векторы – это направленные отрезки, которые помогут вам выразить движение, силу или любое другое векторное величину. Используя их свойства и операции, можно решать разнообразные геометрические задачи, связанные с направлениями и величинами.
• Экспериментальный метод: Подход «попробовать и увидеть» может быть удивительно эффективным, особенно когда стандартные методы не работают. Этот метод включает в себя создание физических или компьютерных моделей для экспериментирования и наблюдения.

В заключение, каждый метод имеет свои сильные и слабые стороны, и выбор метода зависит от конкретной задачи и предпочтений исследователя. Изучив и практикуясь в каждом из них, вы станете настоящим мастером геометрии.

Примеры решения геометрических задач с пошаговыми решениями

В теории геометрии много интересного, но практика – вот где настоящее волшебство. Чтобы показать, как реальные задачи могут быть разрешены с помощью изученных методов, давайте рассмотрим несколько практических примеров с детальным разбором.

Задача на определение площади или периметра геометрической фигуры:

1. • Условие: Дан прямоугольник со сторонами 10 см и 5 см. Найдите его площадь и периметр.
   • Решение:

1. • • Площадь: S=a×b=10×5=50 см^2.
     • Периметр: P=2(a+b)=2(10+5)=30 см.

1. • Ответ: Площадь прямоугольника составляет 50 см^2, а его периметр – 30 см.

Задача на определение углов или сторон фигуры:

1. • Условие: Известно, что два угла треугольника равны 45° и 60°. Найдите третий угол.
   • Решение:

1. • • Сумма углов треугольника равна 180°.
     • Третий угол = 180° — (45° + 60°) = 75°.

1. • Ответ: Третий угол треугольника равен 75°.

Задача на определение радиуса окружности, зная длину её дуги:

1. • Условие: Длина дуги окружности составляет 31.4 см, а угол, который этой дугой заключен, равен 90°. Найдите радиус окружности.
   • Решение:

1. • • Формула длины дуги: l=360°α​×2πr, где α – угол, заключенный дугой, и r – радиус окружности.
     • Из уравнения: 31.4=90/360×2 πr, найдем r.
     • r≈7 см.

1. • Ответ: Радиус окружности равен примерно 7 см.

Задача на использование теоремы Пифагора:

1. • Условие: В прямоугольном треугольнике один катет равен 6 см, а гипотенуза – 10 см. Найдите другой катет.
   • Решение:

1. • • Используя теорему Пифагора: c^2=a^2+b^2, где c – гипотенуза, и a и b – катеты.
     • B^2=10^2−6^2=64.
     • b=8 см.

1. • Ответ: Другой катет равен 8 см.

Полезные инструменты и ресурсы для решения геометрических задач

В эпоху цифровых технологий ручка и бумага, безусловно, остаются незаменимыми инструментами для многих математиков. Однако существует множество современных инструментов и онлайн-ресурсов, которые могут значительно упростить и ускорить процесс решения геометрических задач.

1. GeoGebra – это бесплатное программное обеспечение для математики, объединяющее геометрию, алгебру и анализ в одном пакете. Используйте его для создания интерактивных графиков, исследования геометрических фигур и анализа функций.
2. Desmos Graphing Calculator — єтот бесплатный онлайн-калькулятор позволяет рисовать графики, исследовать функции и проводить анализ данных. Идеально подходит для визуализации и анализа геометрических задач.
3. Wolfram Alpha — комплексный вычислительный движок, который может помочь в решении широкого спектра математических задач, включая геометрию. Вводите свои геометрические задачи и получайте детальные решения шаг за шагом.
4. Сайты с образовательными материалами — ресурсы вроде Khan Academy, Coursera или Udemy предлагают курсы по геометрии с пошаговыми инструкциями и видеоуроками. Подходят для тех, кто хочет глубже изучить геометрию или нуждается в дополнительных ресурсах для практики.
5. 3D-моделирование — программы вроде SketchUp или Tinkercad позволяют создавать 3D-модели геометрических объектов. Применение: Прекрасный способ визуализировать и анализировать пространственные геометрические задачи.
6. Современные технологии предоставляют нам множество инструментов для изучения и практики геометрии. Выберите тот, который лучше всего подходит вашим потребностям, и погрузитесь в увлекательный мир геометрических размышлений.

Заключение

Геометрия — это не просто наука о формах и размерах. Это язык, который позволяет нам понимать и описывать мир вокруг нас. От архитектуры и дизайна до астрономии и медицины, геометрические концепции играют ключевую роль во многих областях науки и искусства.

Через геометрические задачи мы учимся анализировать пространство, развиваем логическое мышление и углубляем понимание математических закономерностей. И, как вы уже узнали, современные инструменты и ресурсы делают процесс решения этих задач еще более интересным и доступным.

Если вы только начинаете свое путешествие в мир геометрии или ищете новые способы улучшить свои навыки, то наши авторы помогут разобраться с задачами по геометрии.